Monkey Business: a dataset of large LLM sample collections for math and code tasks

A monkey maybe solving SWE-bench Lite

TL;DR

We’re releasing the data and code for our recent paper: Large Language Monkeys: Scaling Inference Compute with Repeated Sampling. This includes 10,000 LLM-generated samples per problem for a variety of datasets (GSM8K, MATH, CodeContests, and MiniF2F-MATH) and model families (Llama-3, Gemma, and Pythia)!

LLMs are smart monkeys at keyboards

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, including the complete works of William Shakespeare.

In our paper, we make LLMs our monkeys, exploring whether they can generate correct answers to real-world math and coding datasets when allowed to make hundreds or thousands of attempts. We find that LLMs exhibit inference-time scaling laws where the number of problems solved often increases log-linearly as we scale the number of samples over four orders of magnitude.

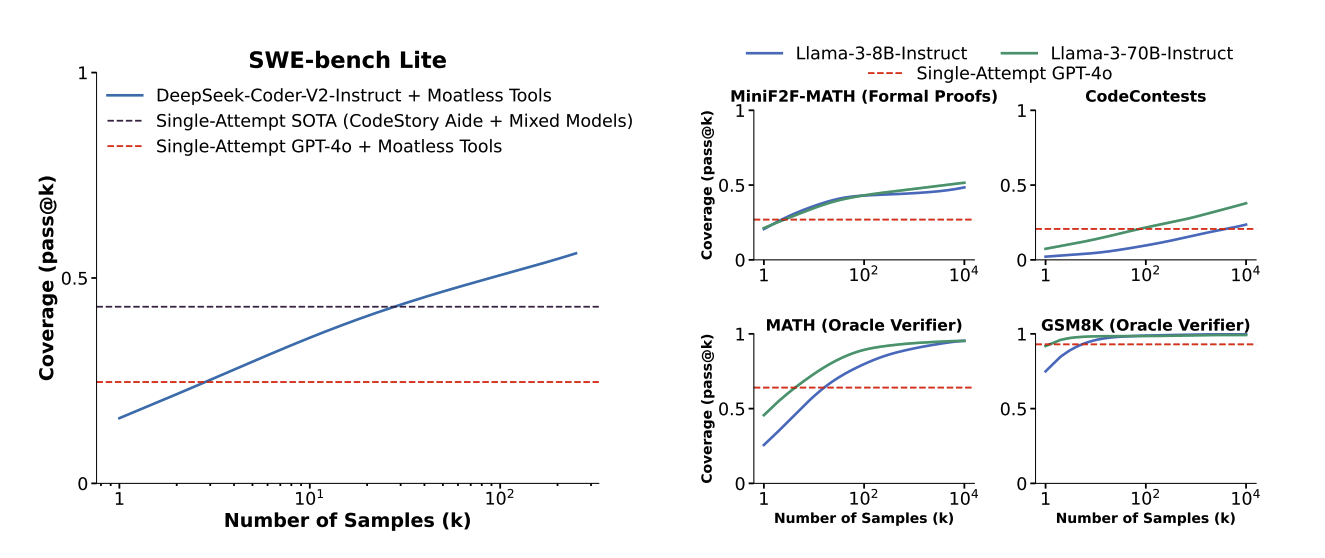
Across five tasks, we find that coverage (the fraction of problems solved by at least one generated sample) increases as we scale the number of samples. Notably, using repeated sampling, we are able to increase the solve rate of an open-source method from 15.9% to 56% on SWE-bench Lite.

The verification problem

When tasks have tools for automatically verifying candidate solutions (ex. formal proof checkers or unit tests for code), we’re done! We can directly benefit from repeated sampling by using our verifiers to pick out correct answers from large sample collections. However, for other datasets, like natural language math problems, identifying a correct answer is less straightforward.

As an initial investigation for how hard verification is in these settings, we compared three simple baselines against oracle selection (ie. choosing the best solution out of k samples):

• Majority voting
• Choosing the sample with the highest score assigned by a reward model
• Majority voting weighted by reward-model scores

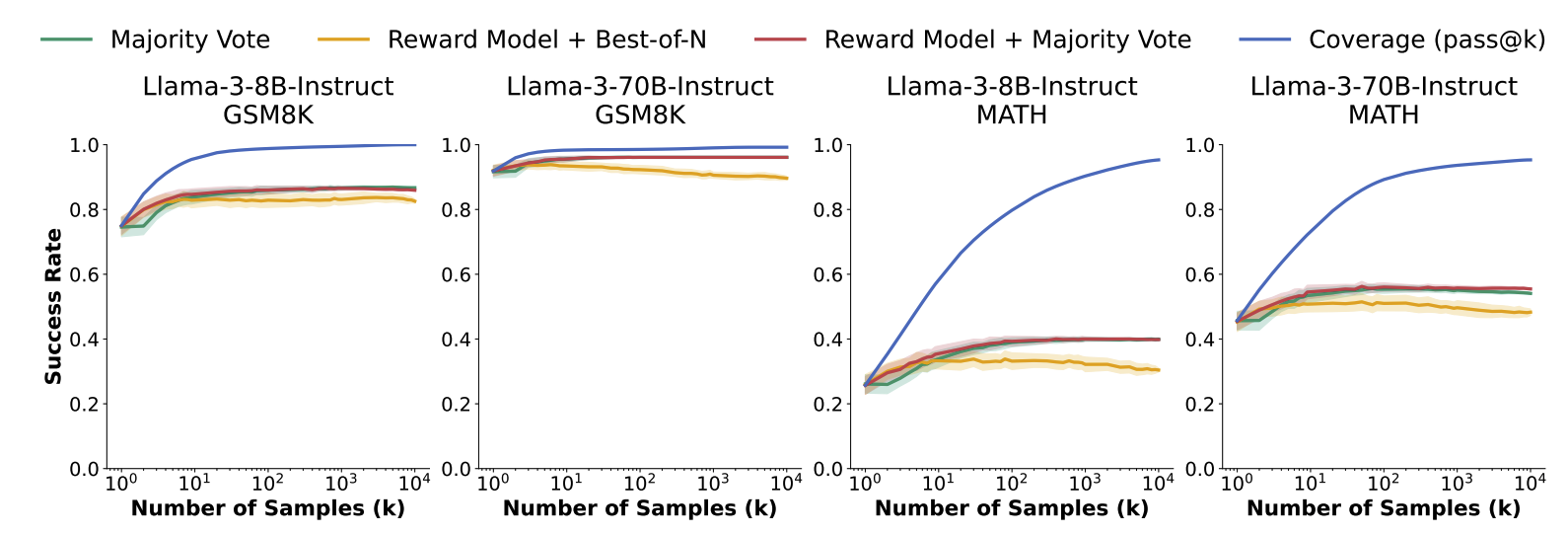
While all three methods improve performance relative to taking a single sample, their performance saturates before 100 samples and falls well below the final oracle accuracy. This gap highlights the importance of continuing to research verification methods.

Monkey Business: A dataset of LLM sample collections

To faciliate verification research in the large sample setting, we are excited to release Monkey Business: a dataset of sample collections for a variety of tasks and models.

Specifically, Monkey Business contains 10,000 correct and incorrect samples per problem for subsets of the following datasets:

• GSM8K: 127 randomly sampled problems from the test set (we originally had 128 but identified a problem with an incorrect ground-truth answer which we removed).
• MATH: 128 randomly sampled problems from the test set.
• CodeContests: all 140 problems in the test set that do not contain images in the problem description.
• MiniF2F-MATH: all 130 problems in the MiniF2F set corresponding to formalized MATH questions.

These samples are generated with the following models:

• GSM8K: Llama-3-8B-Instruct, Llama-3-70B-Instruct
• MATH: Llama-3-8B, Llama-3-8B-Instruct, Llama-3-70B-Instruct, Pythia 70M-12B, Gemma 2B, Gemma 7B
• CodeContests: Llama-3-8B, Llama-3-8B-Instruct, Llama-3-70B-Instruct, Gemma 2B, Gemma 7B
• MiniF2F-MATH: Llama-3-8B-Instruct, Llama-3-70B-Instruct

We are also releasing our sampling and evaluation scripts to make it easier to work with other tasks and models.

🤗 Dataset: https://huggingface.co/datasets/ScalingIntelligence/monkey_business

💻 Github: https://github.com/ScalingIntelligence/large_language_monkeys

In addition to training verifiers, we think that this dataset is useful for several other research directions including self-improvement methods and understanding patterns across correct and incorrect samples.

How to cite? If you use our dataset or code, please cite the following paper:

@misc{brown2024largelanguagemonkeysscaling,
      title={Large Language Monkeys: Scaling Inference Compute with Repeated Sampling}, 
      author={Bradley Brown and Jordan Juravsky and Ryan Ehrlich and Ronald Clark and Quoc V. Le and Christopher Ré and Azalia Mirhoseini},
      year={2024},
      eprint={2407.21787},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2407.21787}, 
}